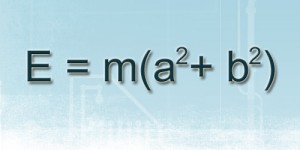Albert Einstein        E=mc^2

Pythagoras             c^2=a^2+b+2

Therefore:             E=m(a^2+b^2)

Albert Einstein (play /ˈælbərt ˈaɪnstaɪn/; German: [ˈalbɐt ˈaɪnʃtaɪn] ( listen); 14 March 1879 – 18 April 1955) was a German-born theoretical physicist who developed the general theory of relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics[2][3] and the most influential physicist of the 20th century. While best known for his mass–energy equivalence formula E=mc^2 (which has been dubbed "the world's most famous equation"),[4] he received the 1921 Nobel Prize in Physics "for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect".[5] The latter was pivotal in establishing quantum theory within physics.

Pythagoras of Samos (Ancient Greek: Πυθαγόρας ὁ Σάμιος [Πυθαγόρης in Ionian Greek] Pythagóras ho Sámios "Pythagoras the Samian", or simply Πυθαγόρας; b. about 570 – d. about 495 BC)[1][2] was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism.

Pythagoras made influential contributions to philosophy and religious teaching in the late 6th century BC. He is often revered as a great mathematician, mystic and scientist, but he is best known for the Pythagorean theorem which bears his name.

Pythagorean theorem
A visual proof of the Pythagorean theorem

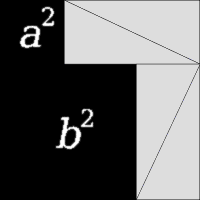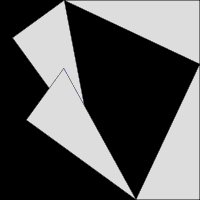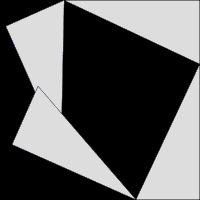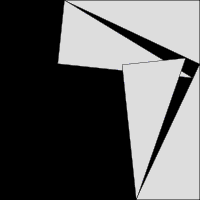Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides—that is, a^2 + b^2 = c^2.

While the theorem that now bears his name was known and previously utilized by the Babylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources.[46] Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta-mathematical problems. Some attribute it as a carefully constructed myth by followers of Plato over two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta-physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck down the centuries up to modern times.[47] The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings of Cicero and Plutarch.

J_\alpha(x) = \sum\limits_{m=0}^\infty \frac{(-1)^m}{m! \, \Gamma(m + \alpha + 1)}{\left({\frac{x}{2}}\right)}^{2 m + \alpha}

Source:  http://en.wikipedia.org/wiki/Pythagoras, http://en.wikipedia.org/wiki/Einstein